Grading on a Curve Hurts Students
Even when it's meant to help them
I’m taking a year off from teaching, and with some of my extra time I’ve enrolled as a student in a physics class. I’m learning a lot, both about physics and about teaching and learning. I’m hoping that being a student again will make me a better teacher and a better textbook author.
A couple weeks ago, we got our first exam back. While she was handing back our exams, our instructor said (paraphrased):
The average score on the exam was 71. If the average had been lower, I would normally offer a “points-back” assignment, but because this class is so large, I don’t have the time to grade it all. Instead, I would have curved the exam grade, but again, the average score was 71, which I’m happy with, so I don’t need to curve it.
I wrote another post about the profound equity implications of my instructor not having enough time to offer the “points-back” assignment. In this post, I reflect on the equity implications of the second option she mention: grading on a curve.
I’ll cut to the chase: Grading on a curve hurts students, even when it’s meant to help them. I’m not the first person to make this argument, but I thought I would summarize what I see as the key critiques of grading on a curve. But first, what is “grading on a curve?”
What is “Grading on a Curve?”
“Grading on a curve” can refer to a few different practices. I discuss a couple of the most common practices here.
In the most traditional sense, grading on a curve means adjusting student grades so the grade distribution follows the Normal Distribution (or “bell curve”). The Normal Distribution is an idealized distribution meant to describe random events like flipping a coin.1 The normal distribution looks like this, where “μ” represents the mean and “σ” represents one standard deviation. The y-axis is frequency of events with that value, e.g. there are many more events with a value close to the mean than values far away from the mean.
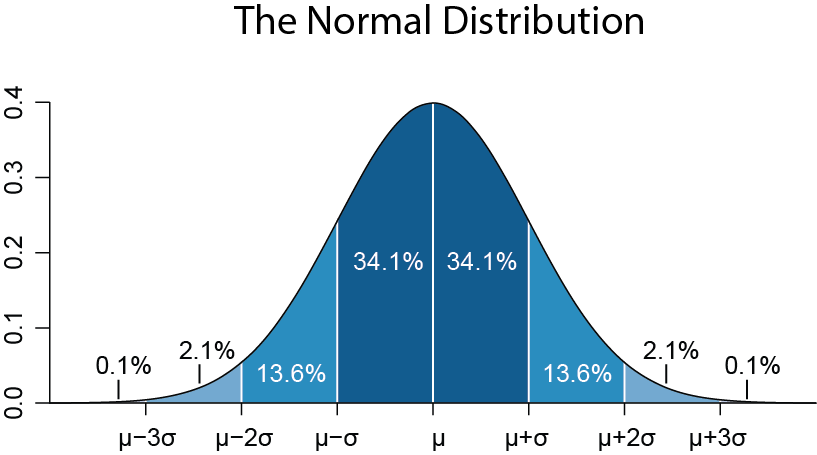
Adjusting course grades to a Normal Distribution means the distribution of grades follows the Normal Distribution, with “C” as the average grade:

In a course graded on a curve, 68% of students get a C. Let’s look at what this means for actual student grades. The following are real final course grades from one of my community college biology courses.
At my institution, we use traditional grade cut-offs, so students who score 90-100 get an A, 80-89 get a B, and so on. In this example, 9 out of 31 (29%) students earned an A.
However, if I were to grade on a curve, I would adjust the distribution to fit the Normal Distribution, so the top 2% of students earn an A, the next 14% of students earn a B, and so on according to the Normal Distribution. Here’s what that would look like:
In this case, it’s obvious that grading on a curve hurts many students: four students who earned 90-91 points are now earning a C instead of an A! And all of the students who earned 80-89 points (typically a B) are now earning a C.
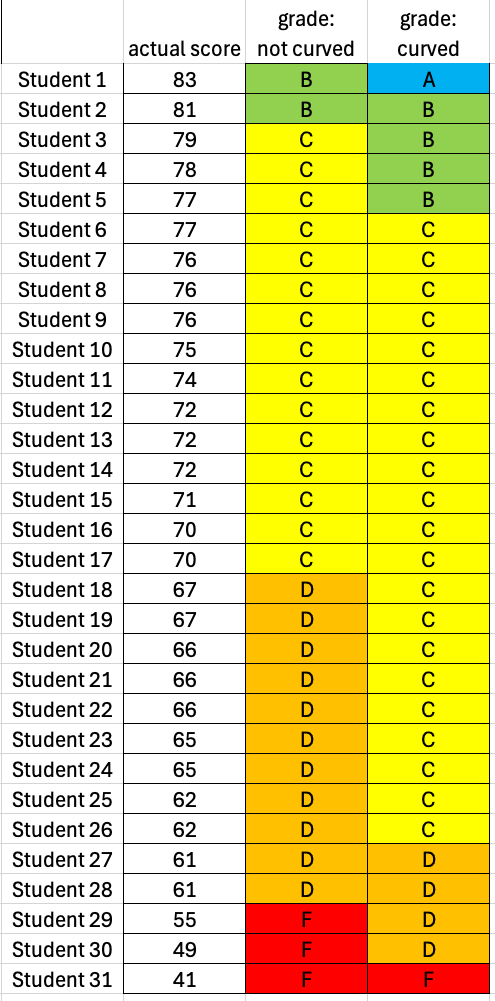
But it’s often the case that instructors grade on a curve to help students, especially when overall scores are low. Let’s consider a different grade distribution with lower overall scores. Note that the high score in this class is 83.
Grading on a curve appears to help many of these students by increasing their grade, so students earning scores in the high 70s now get a B and students earning scores in the 60s get Cs. That’s good, right? It’s not actually (see more below).
It’s worth noting that instructors may use a different curve than the Normal Distribution. For example, an instructor may decide that the top 15% of students earn an A, the next 15% earn a B, etc. This is still considered grading on a curve.
Another way instructors may adjust the grade distribution is to scale the course grades. For example, instructors may add points to everyone’s score. While this results in an adjustment to the distribution of grades, I call it “scaling” because it shifts all the scores according to a scalar value, rather than fitting the grades to a predetermined distribution. Here is an example of scaling grades:
In this case, all students’ scores are shifted up. Again, it seems like this helps students, but it doesn’t.
Grading on a Curve Hurts Students
There are a number of arguments why grading on a curve hurts students. I don’t outline them all here (but see Bowen & Cooper 2021 for a comprehensive list), rather, I outline what I think are the most salient arguments.
Also, a quick note: instructors can grade one assignment or a whole course on a curve. In this post, I refer to final course grades, but the arguments below also apply to grading individual assignments on a curve.
Grading on a curve promotes competition instead of collaboration
If you are a student in a course that is graded on a curve, your grade depends on how your fellow students perform. If you want to earn an A, the last thing you should do is help a classmate, because if they score higher than you, you might lose your chance to earn an A. In fact, you could increase your likelihood of a good grade by sabotaging other students. Yikes. Lots of evidence shows that working with peers (inside or outside of class) improves learning; grading on a curve creates the psychological conditions that discourage this type of collaborative learning.
Grading on a curve divorces the grade from actual student performance
Most people would argue that a grade should represent how well a student demonstrates the content and skills they’ve learned in the course. However, when grades are curved, each student’s grade actually represents that student’s performance relative to other students in the class. This is problematic for several reasons:
The same performance can earn wildly different grades, depending on the other students in the course. As an example, I recently wrote a Letter of Recommendation for a top-notch student, “Chase.” I wanted to write that Chase was one of the top students in the class (he earned 96/100 overall), but in reality, three other students (out of 20) scored higher than him. It turns out, in that semester, 8 out of 20 students earned 95/100 or above. This isn’t grade inflation — it was just a group of really high-achieving students. If I had graded that semester on a curve, some of my truly high-achieving, high-scoring students would have earned a B or even a C simply because there were a lot of other high-achieving students enrolled that semester.
Because the same performance can earn wildly different grades depending on the context, the grade does not provide meaningful information to students about their progress. If I had graded that semester on a curve, Chase would have received a B, sending a signal that he still had gaps in his understanding, which he didn’t.
The opposite can be true too: if all the students in a course score poorly, grading on a curve to raise their scores sends the message that they’ve learned more than they actually have. If all the students in a course are scoring poorly, either the teaching needs to improve, the assessments need to be adjusted, or both.
Grading on a curve automatically assumes some students will fail
Grading on a curve assumes — before the semester even starts — that some percentage of students will fail. This assumption comes from the use of the Normal Distribution to curve grades. Remember that the Normal Distribution describes random events, like coin flips. It turns out, the Normal Distribution is pretty good at describing some continuous variables in biology, like human height or the size of acorns in a population. But human intelligence is not best described by a Normal Distribution, and more importantly, performance in a course is not measuring absolute intelligence, but a mixture of things, including a student’s prior knowledge, the proficiency of the instructor, unexpected life events that affect students’ ability to perform on assessments, skills acquired from well- or poorly-resourced high schools, and on and on. There is no evidence that student proficiency in a course is best described by a Normal Distribution.
I’d like to live in a world where all my students earn A’s. Not because of “grade inflation,” but because they all learned everything I set out for them to learn. Grading on a curve directly opposes this worldview by assuming a predetermined distribution of student proficiency even before the semester begins.
Caveat: We don’t actually know that grading on a curve is inequitable
Recent calls for improving equity in higher education, especially in Science, Technology, Engineering and Math (STEM) courses, have specifically named grading on a curve as problematic for equitable outcomes. Many recent publications specifically link grading on a curve with inequity.2
However, to my knowledge there is no evidence in the literature that grading on a curve perpetuates or worsens inequities. This seems like an obvious gap in the literature.
Note that a lack of evidence does not mean there is no link between inequity and grading on a curve — just that no one has used data to demonstrate the link! It’s worth noting that there is data linking grading on a curve with students feeling discouraged and dropping out of STEM majors (Seymour & Hunter, 2019).
In the physics class I’m enrolled in, my instructor said she would have offered us a points-back assignment on our exam if the average exam score had been lower. But my high exam score pulled up the average! I think it’s unfair that my fellow students didn’t get a chance to have a points-back assignment because they got unlucky enough to be in the same course with me, a PhD scientist enrolled in a introductory physics course.
Not everything you read on the internet was written by a human. For full transparency, here is how I used AI to help me write this post:
I asked Claude to help me illustrate the Normal Distribution and course grade distributions, but its output was terrible, so I made my own illustrations. I also asked it to help me identify the word “continuous variable” when I mentally blanked on the opposite of “discrete variable.” I did not use Claude to help with any other aspect of writing this post.
If you flip a coin 100 times, you should get Heads 50 times. Except you won’t always get 50 heads - you might get 51 Heads, or 47 Heads, which is normal. If you flip a coin 100 times, and repeat that process a bunch of times, you will get 50 Heads on average, but sometimes you’ll get 49 Heads and sometimes you’ll get 42 Heads. You’ll get 49 Heads more often than 42 Heads, and the frequency of getting each event is described by the Normal Distribution.
These are some of the publications that link grading on a curve with inequitable outcomes:
Inclusive Teaching: Strategies for Promoting Equity in the College Classroom (2022) by Kelly Hogan and Viji Sathy
Grading for Equity: What It Is, Why It Matters, and How It Can Transform Schools and Classrooms (2018) by Joe Feldman
Failing our Future: How Grades Harm Students, and What We Can Do about It (2024) by Josh Eyler
Transforming Undergraduate STEM Education: Supporting Equitable and Effective Teaching (2025) by the National Academies of Sciences, Engineering and Medicine
Grading on a Curve as a Systemic Issue of Equity in Chemistry Education (2021) by Ryan Bowen and Melanie Cooper





Great post, as always. Regarding your point, "There is no evidence in the literature that grading on a curve perpetuates or worsens inequities...." It's a reasonable point, yet the arguments against grading on a curve already seem so strong to me that I personally feel no urge to have that data. If I imagine that two empirical studies addressing this issue will be published this summer, I would skim them to see what they found but they wouldn't change my practice one bit. Even if both studies were able to show that grading on a curve did not exacerbate inequity, that would not remotely "redeem" grading on a curve, at least for me.